TL;DR

  • alternates between sampling data through interaction and optimizing a surrogate objective
  • these optimizations are done using mini-batch gradient ascent updates compared to single sample updates in REINFORCE
  • doing multiple updates with same trajectory results in large policy updates which are destructive
  • proposes a new objective function to enable these mini-batch updates
  • implements a clipped surrogate objective which is simpler to implement than TRPO

Background:

Loss function in vanilla policy gradient approach takes following form:

LPG(θ)=Et[log⁡πθ(at∣st)A^t]L^{PG}(\theta) = \mathbb{E}_{t}[\log{\pi_{\theta}(a_t|s_t)}\hat{A}_t]

Add policy gradient derivation

The policy $\pi_{\theta}$ is improved by single step gradient ascent updates on the loss $L^{PG}(\theta)$. Performing multiple steps on the loss leads to large policy updates which are destructive.

In TRPO, we create a surrogate objective with a constraint on the size of policy update.

This constraint theoretically can be added as a penalty term and changed to unconstrained optimization problem.

LTRPO′(θ)=max⁡θEt[πθ(at∣st)πθold(at∣st)A^t−β.KL[πθold(.∣st),πθ(.∣st)]]L^{TRPO'}(\theta) = \max_{\theta} \mathbb{E}_{t}[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t - \beta . KL[\pi_{\theta_{old}}(.|s_t), \pi_{\theta}(.|s_t)]]

understand why KL divergence is calculated in that order, why not the other way? Since $KL[P,Q] \neq KL[Q,P]$

But it is hard to find a single value of $\beta$ which works well across different problems (or over course of learning for one problem).

Clipped Surrogate Objective:

Let us call this Conservative Policy Iteration approach as follows:

LCPI(θ)=Et[rt(θ)A^t]rt(θ)=πθ(at∣st)πθold(at∣st)L^{CPI}(\theta) = \mathbb{E}_{t}[r_t(\theta) \hat{A}_t] \\ r_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}

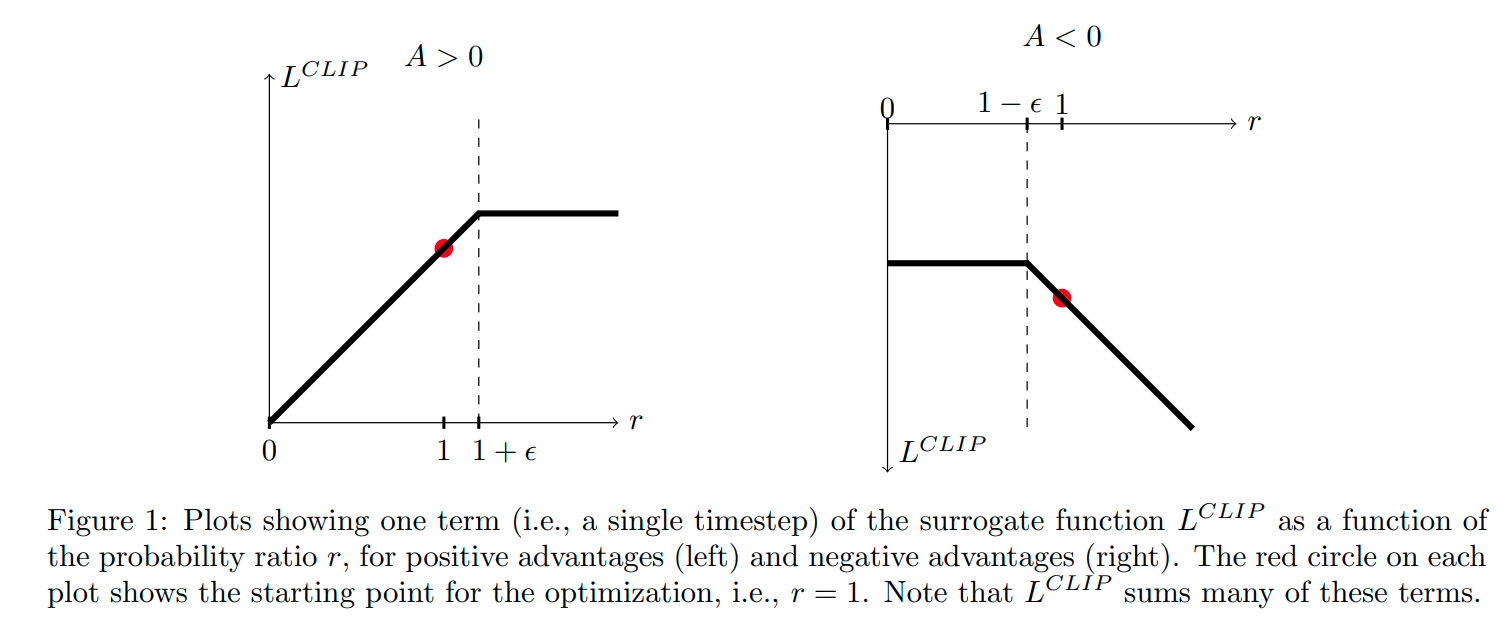
But without a constraint $L^{CPI}$ will result in large destructive policies if the ratio $r_t(\theta)$ becomes very large. We need to penalize changes which move $r_t(\theta)$ away from 1.

LCLIP(θ)=Et[min⁡(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ))A^t]L^{CLIP}(\theta) = \mathbb{E}_t[\min(r_t(\theta)\hat{A}_t, clip(r_t(\theta), 1-\epsilon, 1+\epsilon))\hat{A}_t]

  • First term is same as $L^{CPI}$

  • Second term is a clipped ratio $r_t(\theta)$ in between $(1-\epsilon, 1+\epsilon)$ so that ratio is always close to 1. $\epsilon$ is taken to be 0.2 in the paper.
  • $\min$ is taken to get a lower bound

ppo-clipping

Algorithm Details

PPO-clipped objective with parallel actors and synchronized policy updates.

Network Structure:

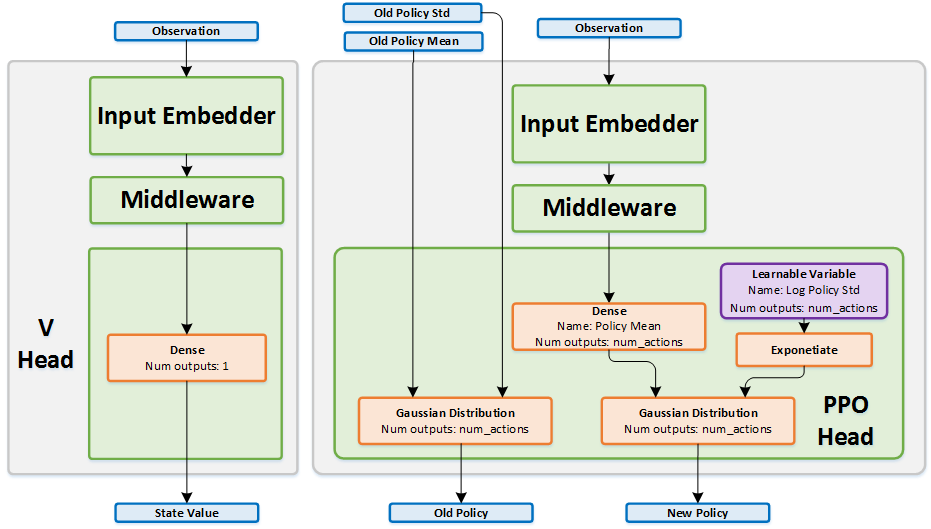
ppo-architecture

Policy Network:

  • input: current state
  • output: mean of a gaussian distribution
  • architecture:
    • Fully connected MLP
    • 2 hidden layers with 64 units
    • tanh non-linearity
    • state independent variable for log stddev (take exponential for getting stddev, this is done to keep the stddev from not becoming too large)

Value Network:

  • input: current state
  • output: value function estimate of the state
  • architecture:
    • Fully connected MLP
    • 2 hidden layers with 64 units
    • tanh non-linearity

Note: Policy and Value networks don’t share parameters as mentioned in the original paper.

Initialize policy parameter $\theta$ and value function parameter $\phi$

for $k$ number of epochs:

​ for parallel actors:

​ Run policy $\pi_{\theta}$ in environment for $T$ timesteps and collect trajectory $D$

​ Compute advantage estimates $\hat{A}t$ based on reward-to-go $\hat{R_t}$ and value function $V{\phi}$

​ Update policy parameter using gradient ascent: θk+1=θk+∇θ1∣D∣T∑τ∈D∑t=0Tmin⁡(πθ(at∣st)πθold(at∣st).A^t,clip(πθ(at∣st)πθold(at∣st),1−ϵ,1+ϵ).A^t)\theta_{k+1} = \theta_{k} + \nabla_{\theta} \frac{1}{|D|T}\sum_{\tau \in D}\sum_{t=0}^{T}{\min{ ( \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}. \hat{A}_t, clip(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}, 1-\epsilon,1+\epsilon).\hat{A}_t})}

​ Update value function parameter using gradient descent: ϕk+1=ϕk−∇ϕ1∣D∣T∑τ∈D∑t=0T(Vϕ(st)−Rt^)2\phi_{k+1} = \phi_{k} - \nabla_{\phi} \frac{1}{|D|T} \sum_{\tau \in D}{ \sum_{t=0}^{T}{ (V_{\phi}(s_t) - \hat{R_t} })^2 }

References: